La tête de perçage vibratoire auto-entretenue

Un des facteurs limitant la productivité des opérations de perçage est l'évacuation du copeau dès que le trou devient trop profond. La mauvaise évacuation et le bourrage du copeau entraînent souvent une mauvaise qualité de la surface usinée pouvant conduire au bris de l'outil. Pour résoudre ce problème,nous avons développé une technique de perçage vibratoire à basse fréquence. Le foret est animé d'un mouvement de vibrations axiales d'amplitude supérieure à l'avance de manière à obtenir des sauts de s'arêtes de coupe hors matière entraînant la fragmentation du copeau. Les copeaux résultants sont de très petites tailles facilitant leurs évacuations. Pour cela, une tête de perçage spécifique a été développée. La génération des vibrations ne nécessite aucun apport extérieur d'énergie ; elles sont générées par l'énergie de la coupe dégagée pendant l'usinage. La stratégie vise à déterminer les conditions de coupe et les paramètres de réglage de la tête permettant d'obtenir ces vibrations. Une modélisation de la tête de perçage permet d'obtenir un diagramme des lobes de stabilité représentant les zones de vibrations et les zones de coupe stable. Une approche expérimentale valide le modèle choisi et permet d'étudier l'influence des paramètres de réglage de la tête sur la génération des vibrations. 

FIG. 1 - La tête de perçage vibratoire auto-entretenue 

1 Introduction

Les opérations de perçage sont des opérations délicates car la coupe est confinée au fonddu trou et les copeaux s'évacuent difficilement. Pour éviter les incidents liés à la mauvaiseévacuation du copeau, les industriels utilisent des cycles de débourrage, cycles consistant àretirer régulièrement le foret de manière à évacuer le copeau. Ces cycles réduisent fortement laproductivité. L'étude de la stabilité en perçage met en évidence des points de fonctionnement oùles broutements axiaux permettent des sauts de l'arête de coupe en dehors de la matière. Dansces conditions, la coupe est discontinue ; le copeau est bien fragmenté et s'évacue facilement.L'étude de la stabilité en usinage est le cœur de nombreuses recherches depuis le début dusiècle dernier. La théorie fondamentale sur l'instabilité a été développée par Tobias & Fishwick,(1958) et Tlusty & Polacek, (1963) qui ont identifié la cause principale : le mécanisme de régénération de la surface. Ces travaux se sont ensuite étendus aux différents process d'usinage et tout particulièrement au fraisage avec Altintas & al (1995). Notre objectif est d'utiliser ces broutements pour augmenter la productivité des opérations de perçage.Plusieurs auteurs de la littérature se sont intéressés à la fragmentation du copeau en perçage. Wang & al (2004) ont étudié le comportement dynamique d'un porte outil équipé d'actionneurs piézoélectriques. Les deux principaux problèmes avec cette solution sont d'avoir des vibrations axiales ayant une amplitude suffisante pour fractionner le copeau et de fournir l'énergie nécessaire sur un porte outil tournant à grande vitesse. Chabra & al (2002) suggère l'utilisation des axes de la machine outil pour créer ces vibrations axiales. Pour obtenir un copeau de petites dimensions, ces vibrations doivent avoir une fréquence supérieure à la fréquence de rotation de l'outil, ce qui sollicite fortement les axes de la machine outil.Nous avons développé une tête de perçage vibratoire(Figure 1) ayant des caractéristiques dynamiques compatibles avec l'apparition de vibrations axiales auto-entretenues et les caractéristiques des outils de coupe.L'objectif étant d'utiliser uniquement l'énergie apportée par la coupe pour générer et maintenir ces vibrations.Cette tête est composée d'un élément qui se monte dans la broche de la machine outil, d'un porte foret qui supporte l'outil et qui est guidé dans le corps et enfin d'un ressort qui est situé entre le corps et le porte foret.

L'objectif de cet article est de proposer un modèle permettant d'identifier les paramètres compatibles avec le fractionnement du copeau. Dans un premier temps, nous nous intéressons à la modélisation dynamique du perçage vibratoire puis dans un deuxième temps à l'identification des points de fonctionnement. La troisième partie décrit la campagne expérimentale ainsi que les possibilités d'ajuster les paramètres de la tête de perçage pour avoir des conditions de coupe proches de celles fournies par le constructeur du foret. Enfin, nous conclurons en mettant en avant les performances actuelles de cette technique. 

2 Modèle dynamique en perçage vibratoire.

2.1 Modèle de la tête de perçage vibratoire

La tête de perçage vibratoire est modélisée par un système du second ordre caractérisé par une masse« m », une raideur« k » et un amortissement visqueux« c » Paris & al (2004)(équation 1). Nous pouvons négliger les autres éléments constituant le système tels que la machine-outil, la pièce et de l'outil car le ressort de la tête a une raideur faible devant la raideur de ces éléments. De plus, il est aussi possible de négliger les vibrations en torsion car la tête de perçage présente une grande raideur en torsion devant la raideur en compression.Cette hypothèse trouve cependant ces limites lorsque le foret aune longueur supérieure à 25 fois le diamètre car la raideur en torsion du foret est alors trop proche de la raideur de la tête pour être négligée. Actuellement, nous travaillons sur la modélisation de ces phénomènes de torsion de manière à les intégrer au modèle dynamique du système usinant

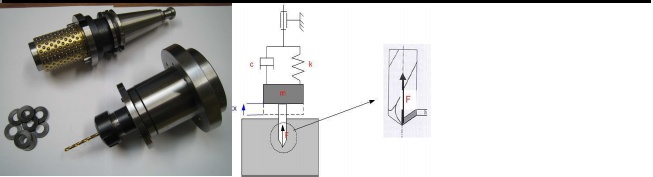
2.2 Modèle d'efforts de coupe

L'effort de poussée est fonction du diamètre du foret D, l'épaisseur de copeau h et d'un coefficient spécifique de coupe Kc qui dépend de la géométrie de la pointe de l'outil (Equation2) : Claudin (2006). Cette partie du foret de par sa géométrie et des vitesses de coupe ne coupe pas la matière de la pièce mais la déforme vers les deux arêtes coupantes du foret : on est en présence d'un phénomène d'extrusion : Guibert & al (2006). Les efforts générés par ce phénomène d'extrusion représentent une part importante de l'effort de poussée. Pour les réduire,les constructeurs d'outil proposent des géométries de pointe de foret spécifiques de manière à réduire l'incidence du phénomène d'extrusion. Tanguy (1993) propose un modèle prenant en compte ces différentes géométries de foret

.F=Kc.D.h

3 Identification des points de fonctionnement A chaque instant, l'épaisseur du copeau h est fonction de la réponse du système usinantaux sollicitations dues à la coupe et de la géométrie usinée lors du passage de l'arête de coupeprécédente. Nous avons donc, sur une représentation par schéma bloc, deux bouclesimbriquées : une correspondant à la réponse du système à l'instantt et l'autre modélisant lephénomène de retard. 

FIG. 3 - Expression de l'épaisseur de copeau par schéma bloc

A partir de ce modèle, Tlusty (1963), Tobias (1958) et Altintas (1995) proposent uneméthode pour calculer les limites de stabilité. Ils obtiennent des lobes de stabilité en fonction durapport de fréquenceF entre la fréquence de passage des arêtes de coupe et la fréquence proprede la tête de perçage vibratoire, et du rapportKp entre la raideur de la tête et la raideur de coupe.Les points de fonctionnement qui nous intéressent sont dans la partie instable (conditionnécessaire). Cependant, pour avoir un saut de l'arête de coupe hors matière, le déphasage entrele comportement du système usinant à l'instant t et le passage de l'arête précédente doit êtreproche de 180°. Il existe donc dans chaque lobe une zone (en gris sur la Figure 4) où cettecondition est atteinte (valeur comprise entre 1,3 et 1,8 pour le 1er lobe).

Pour choisir les conditions opératoires, il est intéressant d'exprimer les limites de stabilitédans un repère lié aux paramètres de la tête de perçage vibratoire (la raideur du ressort« k », lamasse« m ») et la vitesse de rotation« N ». Ces trois paramètres ne sont pas indépendants car lafréquence propre de la tête est fonction de la masse et de la raideur. La figure 5 présente leszones de stabilité pour un perçage de diamètre de 5 mm réalisé avec un foret carbure monoblocdans un acier à vilebrequin 35MnV7. Il est possible de remarquer les différents lobes de stabilité(en rouge le premier lobe, en bleu le deuxième...). Chaque lobe possède ses proprescaractéristiques de vibration (fréquence de vibration) 

a : représentation des lobes en 3D en fonction de lamasse, de la raideur et de la vitesse de rotationb : représentation des lobes pour une masse de 3,25 kg.

FIG. 5 - Les lobes de stabilité en fonction des paramètres de réglage de la tête

4 Validation expérimentalePour valider les concepts et les modèles mis en place, nous avons mené une campagneexpérimentale sur un centre d'usinage Hermle C800V instrumenté. La pièce est montée sur undynamomètre Kistler de manière à suivre l'évolution des efforts de coupe tout au long del'usinage. De plus, un capteur de déplacement inductif sans contact permet de mesurer lesvibrations axiales du foret. Le foret utilisé est un outil en carbure monobloc de diamètre de 5mm avec un affûtage de type pointe en croix. La matière percée est l'acier à vilebrequin35MnV7.4.1 Mise en évidence d'un point de fonctionnementLes lobes de stabilité tracés en Figure 5b montrent que, pour une raideur de 550 N/mm etune masse de 3,25 kg il est possible d'obtenir un perçage vibratoire de qualité avec une vitessede rotation entre 9000 tr/min et 10000 tr/min. Cette configuration dynamique a été testéeexpérimentalement avec la tête de perçage vibratoire avec le foret en carbure monobloc à lavitesse de 9500 tr/min et avec une avance de 0.075 mm/tr. La figure 6 montre les efforts de poussée. L'interruption de la coupe est clairementapparente lorsque l'effort de poussée passe par zéro, prouvant bien l'existence de vibrations.Les efforts s'annulent tous les 10 ms ce qui correspond à une fréquence d'oscillation de 1,7vibrations par tour d'outil. Les copeaux obtenus sont de petites tailles et bien fragmentésLa figure 7 montre le déplacement de la tête. Dans un premier temps le ressort secomprime en fonction de l'augmentation de l'effort de poussée due à la pénétration de la pointedu foret dans la matière. Lorsque l'énergie de coupe est suffisante, les vibrations auto-entretenues apparaissent. Ces vibrations sont « stables » tout au long du perçage. L'instabilitéest donc contrôlée du début à la fin du perçage, il n'y a pas de risque de divergence

L'amplitude de ces vibrations est environ de deux fois l'avance par tour ce qui permet d'obtenirdes sauts hors matière plusieurs fois par tour. A la fin du perçage, la tête reprend sa positiond'équilibre. 

FIG. 6 - Effort de poussée sur 5 tours de foret en perçage vibratoire.

FIG. 7 -. Déplacement de la partie mobile de la tête mesuré par le capteur de déplacement sans contact

4.2 Optimisation du perçage vibratoire en fonction du domaine de fonctionnement del'outilLe tracé des lobes en 3D de la figure 5a montre qu'il est possible en modifiant la masse etla raideur de translater la position de la zone de vibration pour que la vitesse de coupenécessaire à l'obtention des vibrations soit compatible avec le domaine d'utilisation de l'outil.Cette caractéristique se vérifie très bien expérimentalement. Le foret en carbure monobloc a ététesté en perçage vibratoire avec plusieurs raideurs et plusieurs masses. Pour chaqueconfiguration, la recherche d'un domaine de vibration a été menée. Les résultats sont présentéssur la figure 8. On peut remarquer que dans laconfiguration 1, lorsque la masse est de 1,8 kg etla raideur de 550 N/mm (fréquence propre de la tête de 88,0 Hz), le foret se met à vibrer à partirde 8000 tr/min. Dans laconfiguration 2, seule la masse change et est fixée à 3,25 Kg (fréquencepropre de la tête de 65,5 Hz). Dans ce cas, les vibrations apparaissent dès 7000 tr/min. Uneaugmentation de la masse permet donc de baisser la vitesse de rotation d'apparition desvibrations. Il est aussi possible de faire varier la raideur du ressort. Laconfiguration 3 a unemasse de 2,3 Kg et une raideur de 250 N/mm (fréquence propre de la tête de 52,5 Hz). Le débutde la zone de vibration se situe à 6250 tr/min. La modification de la fréquence propre de la têtede perçage en jouant sur la masse et la raideur permet donc d'adapter la position de la zone devibration de manière à la rendre compatible au domaine d'utilisation de l'outil défini par leconstructeur. En augmentant la fréquence propre de la tête, on retarde l'apparition desvibrations. En la diminuant, on facilite la génération des vibrations à faible vitesse. 

FIG. 8 - Comparaison du début de la zone de vibration pour différentes configurations de la tête

5 Conclusions

La technique de perçage vibratoire auto-entretenu est une nouvelle technologie permettant d'augmenter de façon importante la productivité des opérations de perçage. En effet, cette technique permet de percer des trous de grande profondeur (plus de 20 fois le diamètre) sans aucune lubrification, ni cycle débourrage avec des conditions de coupe proches de celles préconisées par le constructeur de l'outil (vitesse de coupe et durée de vie). Les vibrations sont générées par une tête de perçage spécifique brevetée. Cette tête spécifique est utilisable sur tout centre d'usinage. Sa taille et son poids permettent de l'installer dans les magasins d'outils des centres d'usinage et ne nécessite aucun apport d'énergie extérieur. L'utilisation de cette technologie à une application donnée demande un travail suivant 3 phases : la prédiction d'une zone de vibration par étude analytique du perçage vibratoire, l'affinage de la zone de vibration par simulation numérique et enfin une validation expérimentale. L'utilisation de cette technique pour une application de trous profonds permet de réaliser des perçages de 5 mm de diamètre sur 100 mm de profondeur en moins de 8 secondes. La durée de vie de l'outil est garantie sur au moins 25 mètres cumulés à sec. Une étude plus fine et l'optimisation des différents paramètres de la tête et de la géométrie de l'outil devraient permettre de repousser cette limite